三角函数辅助角公式 是怎么求的
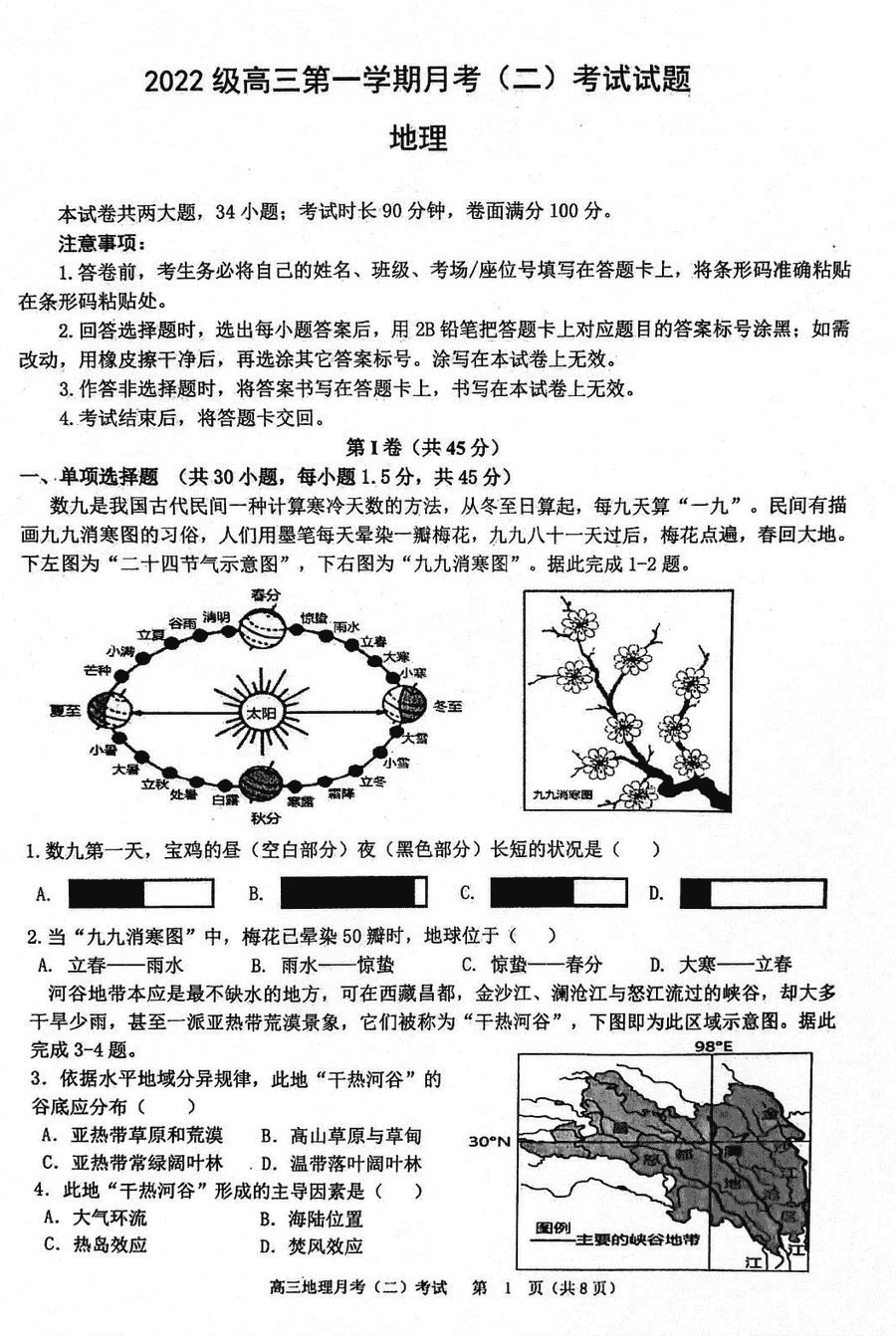
辅助角公式是李善兰先生提出的一种高等三角函数公式,使用代数式表达为asinx+bcosx=√(a²+b²)sin[x+arctan(b/a)](a>0)。

三角函数辅助角公式是什么
asinx+bcosx=√(a+b)sin[x+arctan(b/a)](a>0)。
1.辅助角公式是一种高等三角函数公式,其主要作用是将多个三角函数的和化成单个函数,以此来求解有关最值问题。该公式已被写入中学课本,表达式为asinx+bcosx=√(a+b)sin[x+arctan(b/a)](a>0)。在使用该公式时,无论用正弦还是余弦来表示asinx+bcosx,分母的位置永远是用来表示函数名称的系数。
2.三角函数是基本初等函数之一,是以角度(数学上最常用弧度制,下同)为自变量,角度对应任意角终边与单位圆交点坐标或其比值为因变量的函数。三角函数将直角三角形的内角和它的两个边的比值相关联,也可以等价地用与单位圆有关的各种线段的长度来定义。
3.生活中常见的停车场设计就会用到三角函数,比如在一些形状或地形较为特殊的地段 ,要规划停车场的话,需要用三角函数计算车位和可用车场的面积。食品的外包装问题也是三角函数运用较多的领域,尤其是大包装内部还有独立的小包装,就需要通过三角函数计算出外包装最佳的尺寸,做到既能容纳所有食品,还能做到用料最少。
三角函数万能公式
三角函数的万能公式
sin(a)=[2tan(a/2)]/[1+tan2(a/2)]
cos(a)=[1-tan2(a/2)]/[1+tan2(a/2)]
tan(a)=[2tan(a/2)]/[1-tan2(a/2)]
三角函数的转化公式
sin(-α)=-sinα
cos(-α)=cosα
sin(π/2-α)=cosα
cos(π/2-α)=sinα
sin(π/2+α)=cosα
cos(π/2+α)=-sinα
sin(π-α)=sinα
cos(π-α)=-cosα
sin(π+α)=-sinα
tanα=sinα/cosα
tan(π/2+α)=-cotα
tan(π/2-α)=cotα
tan(π-α)=-tanα
tan(π+α)=tanα
三角函数和差化积公式
sinA+sinB=2sin[(A+B)/2]cos[(A-B)/2]
sinA-sinB=2cos[(A+B)/2]sin[(A-B)/2]
cosA+cosB=2cos[(A+B)/2]cos[(A-B)/2]
cosA-cosB=-2sin[(A+B)/2]sin[(A-B)/2]
tanA+tanB=sin(A+B)/cosAcosB=tan(A+B)(1-tanAtanB)
tanA-tanB=sin(A-B)/cosAcosB=tan(A-B)(1+tanAtanB)