双曲线焦点三角形面积公式

双曲线焦点三角形面积公式：S=b²cot(θ/2)。双曲线有两个焦点。焦点的横（纵）坐标满足c²=a²+b²。

三角形的面积公式

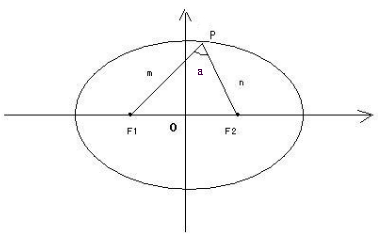
S=1/2PF₁PF₂sinα

=b²sinα/(1-cosα)

=b²cot(α/2)

设∠F₁PF₂=α

双曲线方程为x²/a²-y²/b²=1

因为P在双曲线上,由定义|PF₁-PF₂|=2a

在焦点三角形中,由余弦定理得

F₁F₂²=PF₁²+PF₂²-2PF₁PF₂cosα

=|PF₁-PF₂|²+2PF₁PF₂-2PF₁PF₂cosα

(2c)²=(2a)²+2PF₁PF₂-2PF₁PF₂cosα

PF₁PF₂=[(2c)²-(2a)²]/2(1-cosα)

=2b²/(1-cosα)