自然对数e的意义

自然对数e的意义：自然对数是以常数e为底数的对数，记作lnN（N>0）。在物理学，生物学等自然科学中有重要的意义，一般表示方法为lnx。数学中也常见以logx表示自然对数。

自然对数e意义

超越数主要只有自然常数和圆周率.自然常数的知名度比圆周率低很多,原因是圆周率更容易在实际生活中遇到,而自然常数在日常生活中不常用。

自然对数一般为公式中乘方的底数和对数的底。

自然对数的来法比圆周率简单多了，它就是函数y=f(x)=(1+1/x)x,当x趋向无穷大时y的极限。

同时,它也等于1/0!+1/1!+1/2!+1/3!+1/4!+1/5!+…….同时说明,0!也等于1。

经常在公式中做对数的底.比如,对指数函数和对数函数求导时,就要使用自然常数。函数y=f(x)=ax的导数为f'(x)=ax*ln(a).函数y=f(x)=loga(x)的导数为f'(x)=1/x*ln(10)。

概念

常数e的含义是单位时间内，持续的翻倍增长所能达到的极限值。

自然对数的底e是由一个重要极限给出的。我们定义：当n趋于无穷大时，

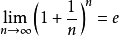
e是一个无限不循环小数，其值约等于2.718281828459…，它是一个超越数。