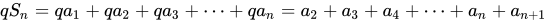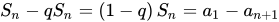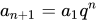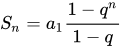等比数列公式及推导
等比数列公式就是在数学上求一定数量的等比数列的和的公式。另外,一个各项均为正数的等比数列各项取同底数数后构成一个等差数列;反之,以任一个正数C为底,用一个等差数列的各项做指数构造幂Can,则是等比数列。

等比数列公式
如果一个数列从第2项起,每一项与它的前一项的比等于同一个常数,这个数列就叫做等比数列。这个常数叫做等比数列的公比,公比通常用字母q表示。
(1)等比数列的通项公式是:
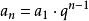
若通项公式变形为
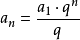
(n∈N*),当q>0时,则可把an看作自变量n的函数,点(n,an)是曲线
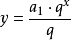
上的一群孤立的点。
(2)任意两项am,an的关系为
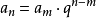
(3)从等比数列的定义、通项公式、前n项和公式可以推出:
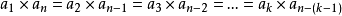
k∈{1,2,…,n}
(4)等比中项:当r满足p+q=2r时,那么则有
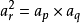
,即ar为ap与aq的等比中项。
等比数列求和公式
求和公式
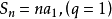
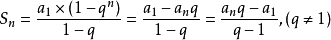
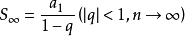
求和公式推导
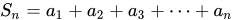
公比为q,