直线和圆的位置关系知识点汇总

2020-10-16 09:21

证明一条直线是圆的切线的常见方法有两种：①当直线和圆有一个公共点时，把圆心和这个公共点连接起来，然后证明直线垂直于这条半径，简称“作半径，证垂直”；②当直线和圆的公共点没有明确时，可过圆心作直线的垂线，再证圆心到直线的距离等于半径。

直线和圆的位置关系

1.直线和圆的位置关系

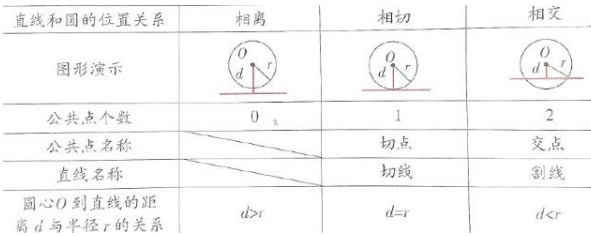
① 相交：直线和圆有两个公共点，这时我们说这条直线和圆相交，这条直线叫做圆的割线。

② 相切：直线和圆只有一个公共点，这时我们说这条直线和圆相切，这条直线叫做圆的切线，这个点叫做切点。

③ 相离：直线和圆没有公共点，这时我们说这条直线和圆相离。

④ 直线和圆的位置关系

2.圆的切线

① 切线的判定定理：经过半径的外端并且垂直于这条半径的直线是圆的切线。如图，直线l就是⊙O的切线。此外，经过圆心且垂直于切线的直线一定过切点；垂直于切线且过切点的直线必过圆心。

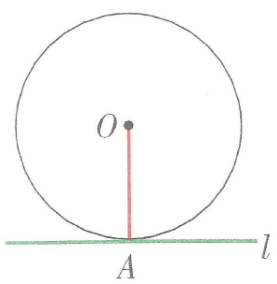
② 切线的性质定理圆的切线垂直于过切点的半径。如上图，若直线l是⊙O的切线，A为切点，则l丄OA.

3. 切线长

① 切线长：经过圆外一点的圆的切线上，这点和切点之间的线段的长，叫做这点到圆的切线长。

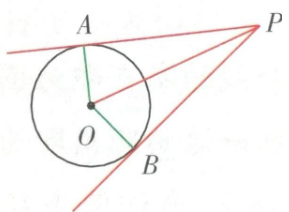
② 切线长定理：从圆外一点可以引圆的两条切线，它们的切线长相等，这一点和圆心的连线平分两条切线的夹角.如图，PA，PB是⊙O的两条切线，B切点分别为A，B，则PA=PB，∠OPA=∠OPB.

4.切线的判定和性质的应用

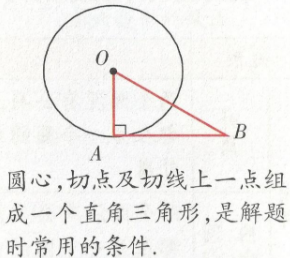
(1)辅助线的作法运用切线的性质来进行计算或论证的常见辅助线是连接圆心和切点，利用垂直构造直角三角形解决有关问题。

(2) 证明直线与圆相切的三种途径

证直线和圆有唯一公共点（即运用定义）①.证直线过半径外端且垂直于这条半径（即运用判定定理）②.证圆心到直线的距离等于圆的半径（即证d=r)③.

当题目已知直线与圆的公共点时，一般用方法②，当题目未知直线与圆的公共点时，一般用方法③，方法①运用较少。

1、代数法:

联立直线方程和圆方程，解方程组，方程组无解，则直线与圆相离，方程组有1组解，则直线与圆相切，方程组有2组解，则直线与圆相交。

2、几何法:

求出圆心到直线的距离d，半径为r。d>r，则直线与圆相离，d=r，则直线与圆相切，d<r，则直线与圆相交。