2021年宁夏高考理科数学真题
2021年普通高等学校招生全国统一考试
理科数学乙卷
注意事项:
1.答卷前,考生务必将自己的姓名、准考证号填写在答题卡上。
2.回答选择题时,选出每小题答案后,用铅笔把答题卡上对应题目的答案标号涂黑。如需改动,用橡皮擦干净后,再选涂其他答案标号。回答非选择题时,将答案写在答题卡上。写在本试卷上无效。
3.考试结束后,将本试卷和答题卡一并交回
一、选择题:本题共12小题,每小题5分,共60分。在每小题给出的四个选项中,只有一项是符合题目要求的。
1.设2(z+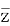 )+3(z-
)+3(z-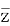 )=4+6i,则z=( ).
)=4+6i,则z=( ).
A.1-2i
B.1+2i
C.1+i
D.1-i
2.已知集合S={s|s=2n+1,n∈Z},T={t|t=4n+1,n∈Z},则S∩T=( )
A.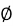
B.S
C.T
D.Z
3.已知命题p: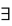 x∈R,sinx<1;命题q:
x∈R,sinx<1;命题q: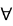 x∈R,
x∈R,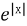 ≥1,则下列命题中为真命题的是( )
≥1,则下列命题中为真命题的是( )
A.p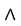 q
q
B.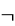 p
p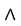 q
q
C.p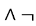 q
q
D.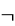 (pVq)
(pVq)
4.设函数f(x)=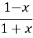 ,则下列函数中为奇函数的是( )
,则下列函数中为奇函数的是( )
A.f(x-1)-1
B.f(x-1)+1
C.f(x+1)-1
D.f(x+1)+1
5.在正方体ABCD-A1B1C1D1中,P为B1D1的中点,则直线PB与AD1所成的角为( )
A.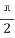
B.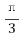
C.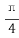
D.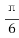
6.将5名北京冬奥会志愿者分配到花样滑冰、短道速滑、冰球和冰壶4个项目进行培训,每名志愿者只分到1个项目,每个项目至少分配1名志愿者,则不同的分配方案共有( )
A.60种
B.120种
C.240种
D.480种
7.把函数y=f(x)图象上所有点的横坐标缩短到原来的 倍,纵坐标不变,再把所得曲线向右平移
倍,纵坐标不变,再把所得曲线向右平移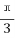 个单位长度,得到函数y=sin(x-
个单位长度,得到函数y=sin(x- )的图像,则f(x)=( )
)的图像,则f(x)=( )
A.sin(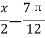 )
)
B. sin(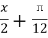 )
)
C. sin(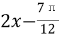 )
)
D. sin(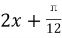 )
)
8.在区间(0,1)与(1,2)中各随机取1个数,则两数之和大于 的概率为( )
的概率为( )
A.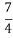
B.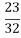
C.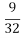
D.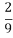
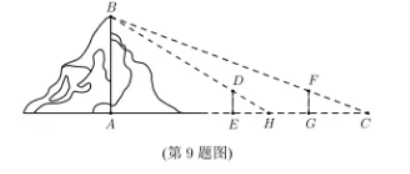
9.魏晋时期刘徽撰写的《海岛算经》是关于测量的数学著作,其中第一题是测量海盗的高。如图,点E,H,G在水平线AC上,DE和FG是两个垂直于水平面且等高的测量标杆的高度,称为“表高”,EG称为“表距”,GC和EH都称为“表目距”,GC与EH的差称为“表目距的差”。则海岛的高AB=( ).
A:
B:
C:
D:
10.设a≠0,若x=a为函数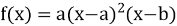 的极大值点,则( ).
的极大值点,则( ).
A:a<b
B:a>b
C:ab<a2
D:ab>a2
11.设B是椭圆C: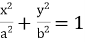 (a>b>0)的上顶点,若C上的任意一点P都满足
(a>b>0)的上顶点,若C上的任意一点P都满足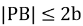 ,则C的离心率的取值范围是( ).
,则C的离心率的取值范围是( ).
A: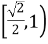
B: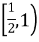
C: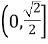
D: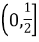
12.设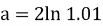 ,
,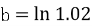 ,
,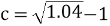 ,则( ).
,则( ).
A:a<b<c
B:b<c<a
C:b<a<c
D:c<a<b
二、填空题:本题共4小题,每小题5分,共20分。
13.已知双曲线C: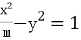 (m>0)的一条渐近线为
(m>0)的一条渐近线为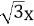 +my=0,则C的焦距为 .
+my=0,则C的焦距为 .
14.已知向量a=(1,3),b=(3,4),若(a-λb)⊥b,则λ= 。
15.记△ABC的内角A,B,C的对边分别为a,b,c,面积为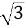 ,B=60°,a2+c2=3ac,则b= .
,B=60°,a2+c2=3ac,则b= .
16.以图①为正视图和俯视图,在图②③④⑤中选两个分别作为侧视图和俯视图,组成某个三棱锥的三视图,则所选侧视图和俯视图的编号依次为 (写出符合要求的一组答案即可).
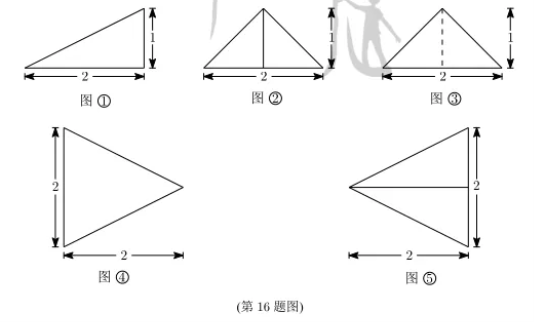
三、解答题:共70分。解答应写出文字说明、证明过程或演算步骤。第17-21题为必考题,每个试题考生都必须作答。第22、23题为选考题,考生根据要求作答。
(一)必考题:共60分。
17.(12分)
某厂研究了一种生产高精产品的设备,为检验新设备生产产品的某项指标有无提高,用一台旧设备和一台新设备各生产了10件产品,得到各件产品该项指标数据如下:
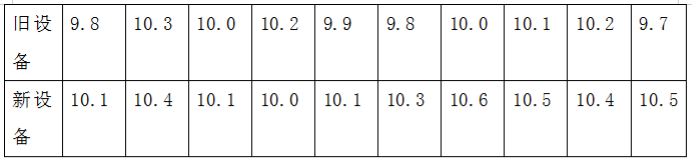
旧设备和新设备生产产品的该项指标的样本平均数分别记为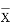 和
和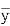 ,样本方差分别记为s12和s22
,样本方差分别记为s12和s22
(1) 求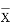 ,
,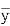 , s12,s22;
, s12,s22;
(2) 判断新设备生产产品的该项指标的均值较旧设备是否有显著提高(如果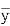 -
-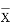 ≥
≥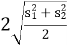 ,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
,则认为新设备生产产品的该项指标的均值较旧设备有显著提高,否则不认为有显著提高).
18.(12分)
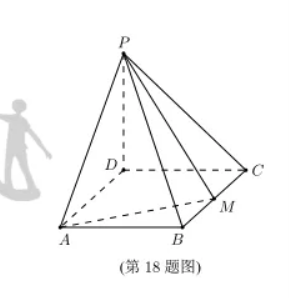
如图,四棱锥P-ABCD的底面是矩形,PD⊥底面ABCD,PD=DC=1,M为BC的中点,且PB⊥AM,
(1) 求BC;
(2) 求二面角A-PM-B的正弦值。
19.(12分)
记S n为数列{an}的前n项和,bn为数列{Sn}的前n项和,已知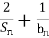 =2.
=2.
(1) 证明:数列{bn}是等差数列;
(2) 求{an}的通项公式.
20.(12分)
设函数f(x)=ln(a-x),已知x=0是函数y=xf(x)的极值点。
(1) 求a;
(2) 设函数g(x)=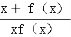 ,证明:g(x)<1.
,证明:g(x)<1.
21.(12 分)
己知抛物线C:x2=2py(p>0)的焦点为F,且F与圆M:x2+(y+4)2=1上点的距离的最小值为4.
(1)求p;
(2)若点P在M上,PA,PB是C的两条切线,A,B是切点,求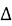 PAB的最大值.
PAB的最大值.
(二)选考题:共10分,请考生在第22、23题中任选一题作答。如果多做,则按所做的第一题计分。
22.[选修4一4:坐标系与参数方程](10分)
在直角坐标系xOy中, C的圆心为C(2,1),半径为1.
C的圆心为C(2,1),半径为1.
(1)写出 C的一个参数方程;的极坐标方程化为直角坐标方程;
C的一个参数方程;的极坐标方程化为直角坐标方程;
(2)过点F(4,1)作 C的两条切线, 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求这两条直线的极坐标方程.
C的两条切线, 以坐标原点为极点,x轴正半轴为极轴建立极坐标系,求这两条直线的极坐标方程.
23.[选修4一5:不等式选讲](10分)
已知函数f(x)=|x-a|+|x+3|.
(1)当a=1时,求不等式f(x)≥6的解集;
(2)若f(x)≥ —a ,求a的取值范围.






